K-최근접 이웃 알고리즘 (KNN, K-Nearest Neighbor Algorithm)

• KNN 알고리즘은 input_data로부터 거리가 가까운 k개의 다른 데이터의 레이블을 참조하여 분류하는 알고리즘
• 거리를 측정할 때 유클리디안 거리 계산법을 활용
• 거리기반의 모델들은 변수 값을 표준 범위로 재조정하기 위한 정규화(normalize)가 필수
• KNN 간단하지만 이미지 처리, 글자 인식, 영화나 음악 추천 알고리즘 등 많은 분야에서 사용됨

위의 이미지에서 볼 수 있듯이 유사한 데이터 포인트끼리 서로 거리가 가깝다는 것을 알 수 있습니다. KNN은 이러한 가정으로부터 고안된 알고리즘입니다. KNN은 주변 이웃의 분포에 따라 예측 결과를 예측하는데 가장 단순한 결정 방식은 다수결(Majority voting)입니다. 이웃들 범주 가운데 빈도 기준 제일 많은 범주로 새 데이터의 범주를 예측하는 것입니다. 만약 k개중에 동률이 발생하면 입력 데이터와 가장 가까운 범주로 예측을 하거나 랜덤으로 하나를 고를 수 있습니다.

다른 방식으로는, 가중합(weighted voting) 방식도 있습니다. 거리(d)가 가까운(=유사도가 높은) 이웃의 정보에 좀 더 가중치를 줍니다. 1/(1+d), 1/(1+d2), exp(−d) 등 가중치를 통해서 범주를 예측할 수 있습니다.

KNN의 하이퍼 파라미터는 k(탐색할 이웃 수)와 거리 측정 방법 두 가지 입니다. k값이 작을 경우 데이터의 직역적 특성에 민감하게 반영되어 overfitting의 위험이 있고, 반대로, k값이 너무 클 경우 지나치게 정규화 되어 underfitting의 위험이 있습니다. 아래 그림처럼 k값의 크기에 따라(k=1, k=15) 경계면이 단순해지는 것을 확인할 수 있습니다.

데이터 포인트 간의 거리 측정 방법은 여러가지 있지만, 일반적으로 대중적인 유클리디안 거리를 많이 사용합니다. (거리 지표: Euclidean Distance, Manhattan Distance, Mahalanobis Distance etc.)

• 유클리디안 거리: n차원의 공간에서 두 점간의 거리를 알아내는 방식

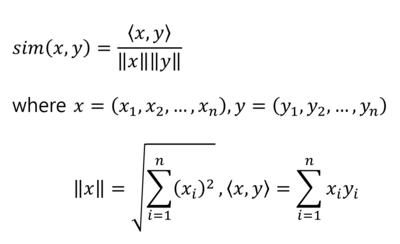
최적의 K값

최적의 K값은 데이터셋마다 다르기 때문에 가장 적합한 k를 찾기 위해서는 k의 범위를(ex. 1~100) 지정하고, 각 k에 대하여 KNN알고리즘을 여러 번 실행하여 오차가 가장 적게 나오는 k값을 선택해야 합니다. 학습데이터와 검증데이터(validation data)를 나누고, k값을 늘려가면서 Error rate의 변화를 확인할 수 있습니다.

KNN 장단점

• 장점
  • 알고리즘이 간단하고 구현하기 쉬움
  • 모델을 구축하거나 여러 매개변수를 조정할 필요가 없음
  • 알고리즘이 다양해서 분류, 회귀 및 검색에 사용할 수 있음
  • 노이즈에 영향을 크게 받지 않음
• 단점
  • 데이터(학습데이터, 테스트 데이터) 수가 증가함에 따라 상당히 느려짐
  • 변수의 개수, Fiture의 개수가 많을 경우 KNN의 성능이 떨어질 수 있음

정리

KNN 알고리즘은 분류, 회귀 문제를 해결하는데 사용할 수 있는 간단한 지도학습 머신러닝 알고리즘입니다. 구현하고 이해하기 쉽지만 데이터 양이 많아질수록 속도가 크게 느려진다는 KNN의 단점은 빠르게 예측을 해야 하는 환경에서 비실용적인 방안일 수 있습니다. 그러나 예측에 사용하는 데이터를 신속하게 처리할 수 있는 충분한 컴퓨팅 리소스가 있는 경우 KNN은 유사한 개체 식별이 요구되는 솔루션에서 여전히 잘 사용되고 있다고 합니다.