SVM(Support Vector Machine)

• SVM은 Support Vector와 Hyperplane(초평면) 이용하여 분류를 하는 알고리즘
• SVM: 서포트 벡터 머신, Support Vector Machine
  • SVC: Support Vector Classifier, 범주형 변수일 경우
  • SVR: Support Vector Regression, 연속형 변수일 경우
  • 보통 SVM 자체는 범주형 변수일 때를 일컫습니다.

SVM의 목적은 두 개의 다른 클래스를 가장 잘 분류할 수 있는 결정 경계(Decision Boundary)를 찾는 것입니다.
잘 분류한다는 것(결정 경계의 조건)은 서포트 벡터(Support Vector)로부터 거리가 가장 먼 결정 경계를 찾는 것인데(Margin이 가장 큰 값일 때)
어느 한쪽에 치우치지 않게 하며, 빈 공간이라도 양쪽 군집과 균등한 위치에 있어야 합니다.

결정 경계(Decision Boundary)

• 클래스를 분류하기 위한 경계
• 2차원의 결정 경계는 선, 3차원은 평면, 그 이상은 초평면(Hyperplane)이라고 부릅니다.
  • 초평면은 시각적으로 표시할 수 없음

마진(Margin)

• 마진(margin): 결정 경계와 서포트 벡터 사이의 거리
• 서포트 벡터는 결정 경계와 가장 가까이 있는 데이터 Vector들을 의미합니다.

SVM은 데이터들을 올바르게 분리하면서 마진의 크기를 최대화해야 하기 때문에, 이상치(Outlier)들을 잘 다루는게 중요합니다.
여기서 하드 마진(Hard margin)과 소프트 마진(Soft margin)이라는 개념이 나옵니다.

• 하드 마진
  • 결정 경계와 서포트 벡터의 거리가 좁은 마진
  • 과적합(Overfitting)을 야기할 수 있음
• 소프트 마진:
  • 결정 경계와 서포트 벡터의 거리가 넓은 마진
  • 과소적합(Underfitting)을 야기할 수 있음

하드마진 VS 소프트마진
데이터 세트가 선형으로 분리 될 때 소프트 마진 SVM이 더 좋아질 것으로 기대합니다. 하드 마진 SVM에서 단일 이상치가 경계를 결정할 수 있기 때문에 분류자가 데이터의 노이즈에 지나치게 민감하게 만들기 때문입니다.

• 하드 마진을 할 경우 빨간색 이상치가 경계를 결정하며 과적합을 일으키는 경우

커널(Kernel)

선형으로 분리할 수 있는 경우와 그렇지 않은 경우가 있는데 지금까지는 선형으로 분리할 수 있는 경우의 예시만 보여드렸습니다.
선형으로 분리할 수 없는 경우에는 비선형 SVM을 써야 하는데 어떻게 구축할 수 있을지가 핵심이고 관측 데이터들을 더 높은 차원의 데이터로 변환시켜서 분류해 보자는 아이디어가 제시되었습니다.

• 커널 기법은 데이터를 더 높은 차원으로 이동시켜 데이터를 분류하는 방법
• 커널 종류: 선형, 다항식, 가우시안, 시그모이드(Sigmoid)

1. 다항식(Polynomial)

• (x,y)처럼 2차원의 좌표를 3차원의 좌표로 변환
• 더 높은 차원으로 변형하여 초평면 결정 경계를 얻을 수 있음

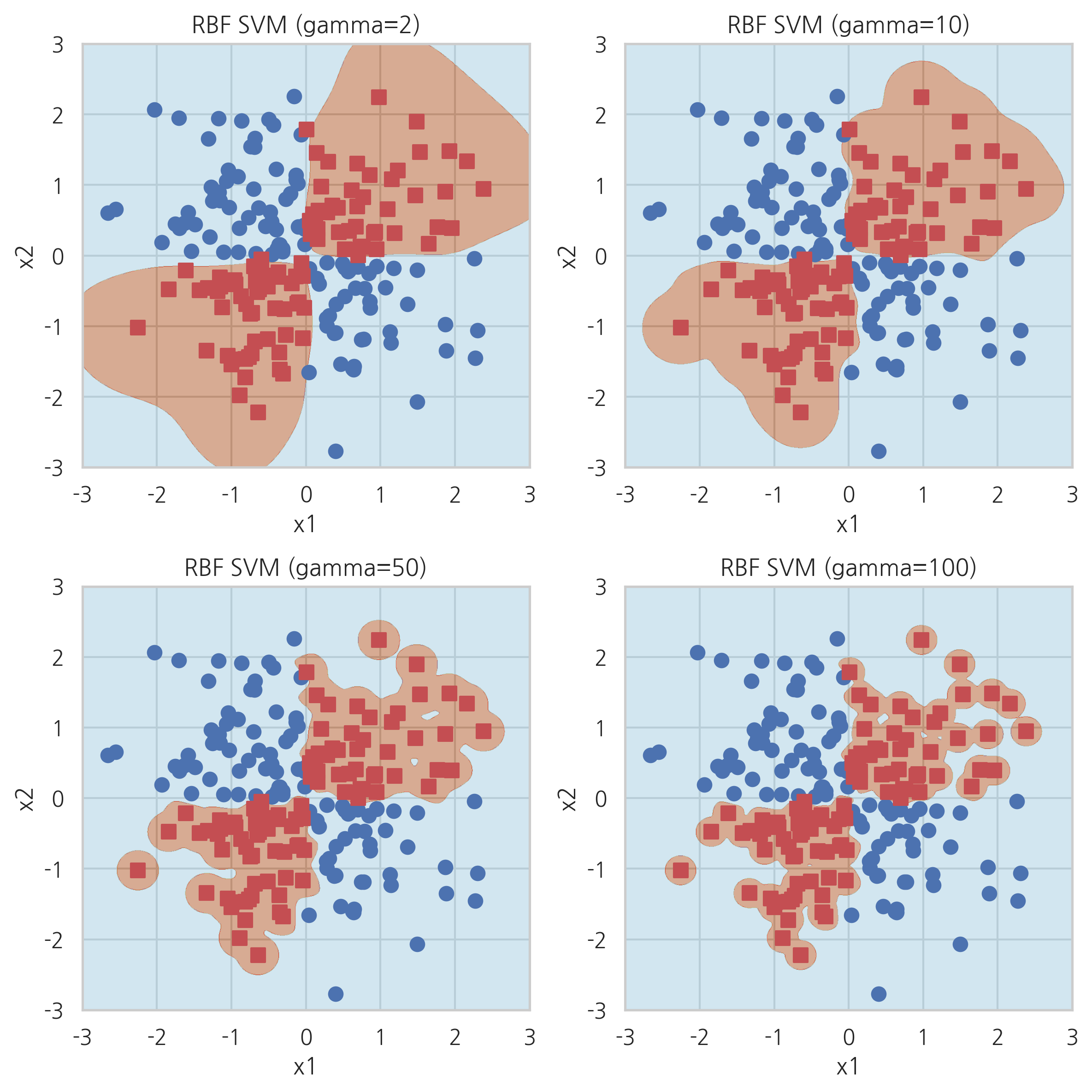
2. 가우시안 커널(RBF: Radial Bias Function, Gaussian kernel)

• 성능이 우수하여 가장 많이 쓰이는 기법
• 2차원의 좌표를 무한한 차원의 좌표로 변환
• gamma: SVM 가우시안 커널의 파라미터
  • 값이 클수록 유연 -> 오버피팅 위험
  • 값이 작을수록 뻣뻣 -> 언더피팅 위험

정리

• SVM은 서포트 벡터(Support Vector)로부터 Margin이 가장 큰 결정 경계(Decision Boundary)를 찾아 두 클래스를 분류하는 알고리즘
• 고차원 데이터의 분류문제의 좋은 성능을 보임
• 범주형 데이터, 수치형 데이터의 분류 문제에 사용 가능
• 예측이 어떻게 결정되었는지 이해하기 어렵고 모델을 분석하기도 어려움

REFERENCE

https://hleecaster.com/ml-svm-concept/
https://techblog-history-younghunjo1.tistory.com/78
김성범 [핵심 머신러닝]SVM모델