트리(Tree)
-
정점과 간선을 이용해 사이클을 이루지 않도록 구성한 Graph의 특수한 형태로, 계층이 있는 데이터를 표현하기에 적합하다.
-
용도
- 계층적 데이터 저장
- 트리 중 이진 트리 형태의 구조로, 탐색(검색) 알고리즘 구현을 위해 많이 사용됨
- 힙(Heap)
- 데이터베이스 인덱싱(데이터베이스 인덱싱을 구현하는데 트리를 사용, B-Tree, B+Tree, AVL-Tree)
- Trie (= Prefix Tree, 사전을 저장하는 데 사용되는 특별한 종류의 트리)
이진 트리(Binary Tree)
- 각 노드가 최대 두 개의 자식을 갖는 트리
- 이진 트리의 순회는 재귀 호출을 사용한다. 따라서 전위, 중위, 후위 순회를 간단하게 구현할 수 있다.
- 순회란 모든 원소를 빠트리거나 중복하지 않고 처리하는 연산을 의미한다.
- 용도
- 수식트리(Expression Tree)
- 허프만 트리(Huffman Tree)
- 이진검색 트리 (BST, Binary Search Tree)
- 우선 순위 큐(PQ)
class Node(object):
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def __str__(self):
return str(self.data)
class BinaryTree():
def __init__(self, root):
self.root = Node(root)
# DLR
def preorder(self, node:Node, result:list):
result.append(node.data)
if node.left: self.preorder(node.left, result)
if node.right: self.preorder(node.right, result)
return result
# LDR
def inorder(self, node:Node, result:list):
if node.left: self.inorder(node.left, result)
result.append(node.data)
if node.right: self.inorder(node.right, result)
return result
# LRD
def postorder(self, node:Node, result:list):
if node.left: self.postorder(node.left, result)
if node.right: self.postorder(node.right, result)
result.append(node.data)
return result
스레드 이진 트리
- 이진 트리는 시스템 혹은 외부 스택을 관리해야하며 하위 레벨로 내려갈수록 재귀 호출의 깊이가 깊어져 비효율적일 수 있다.
- 이진 트리의 순회구현은 간단하지만 성능적인 측면은 좋다고 할 수 없음
- 스레드 이진 트리는 재귀 호출 없이 순회할 수 있도록 구현된 트리이다.
- 가리키는 곳이 없는 모든 오른쪽 널 포인터를 중위 후행자 노드로 연결한 것

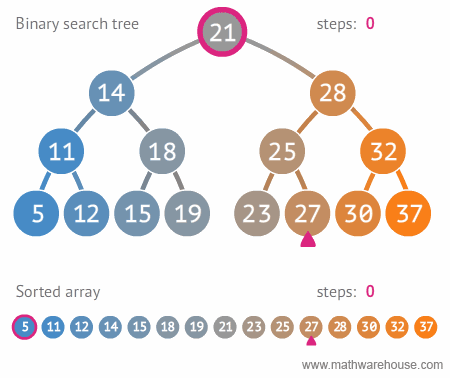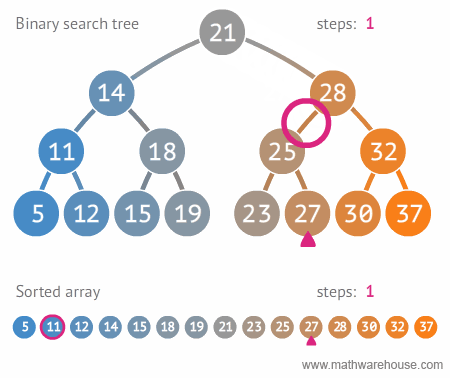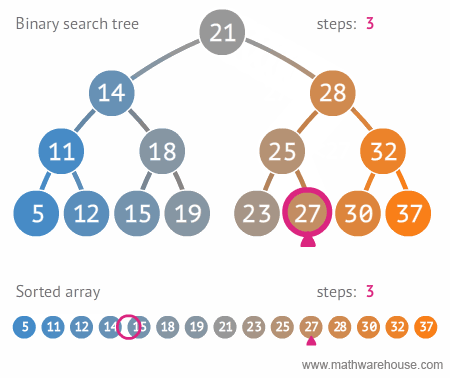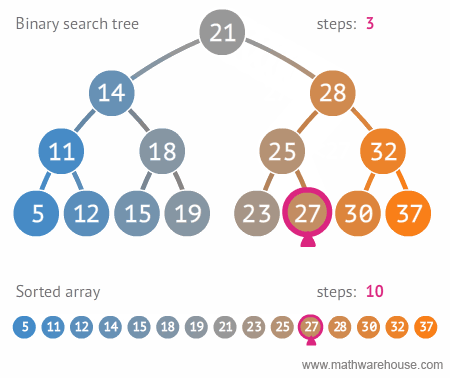
이진 탐색 트리
- 트리를 효율적으로 구현하고 사용하기 위해서 일정한 조건으로 정의한 것
- 모든 왼쪽 자식들 <= n < 모든 오른쪽 자식들 (모든 노드 n에 대해서 반드시 참)
- 용도: 데이터 탐색 -> 평균 탐색 속도 O(logn)
def insert(self, node:Node, data):
if node is None:
node = Node(data)
else:
if node.data > data: node.left = self.insert(node.left, data)
elif node.data < data: node.right = self.insert(node.right, data)
return node
- 이진 탐색 트리의 삭제
- 삭제할 노드가 Leaf Node인 경우
- parent node가 노드를 가르키지 않도록 함

- 삭제할 노드의 자식이 하나인 경우
- 노드를 삭제하고 자식 노드를 삭제된 노드의 부모에 직접 연결

-
삭제할 노드의 자식이 둘인 경우
- 삭제할 노드를 찾는다
- 삭제할 노드의 successor 노드를 찾는다 (successor 노드: right subtree의 최소값)
- 삭제할 노드와 successor 노드의 값을 바꾼다
- successor 노드를 삭제

def delete_node(self, current_node, value):
# 노드 찾기
if current_node is None:
return None
if current_node.data > value:
current_node.left = self.delete_node(self, current_node.left, value)
return current_node
elif current_node.data < value:
current_node.right = self.delete_node(self, current_node.right, value)
return current_node
else: #current.value == data
if (current_node.left is None) and (current_node.right is None):
# case 1
return None
elif current_node.left is None:
# case 2-1 오른쪽 자식만 있을 때
return current_node.right
elif current_node.right is None:
# case 2-2 왼쪽 자식만 있을 때
return current_node.left
else:
# 자식이 둘 다 있는 경우
# 3-2 successor node 찾기
successor_node = current_node.right
while successor_node.left is not None:
successor_node = successor_node.left
current_node.data = successor_node.data # 3-3
current_node.right = self.delete_node(current_node.right, successor_node.data) # 3-4
return current_node
AVL 트리
- 편향트리를 해결하기 위한 것
- 이진 탐색 트리는 좌우 균형이 잘 맞으면 탐색 성능이 높아진다.
- BF = hL-hR (왼쪽 서브트리 높이에서 오른쪽 서브트리를 뺀 값)
- 어떤 시점에서 높이 차이(BF)가 1보다 커지면 회전(rotation)을 통해 균형을 잡아 높이 차이를 줄임
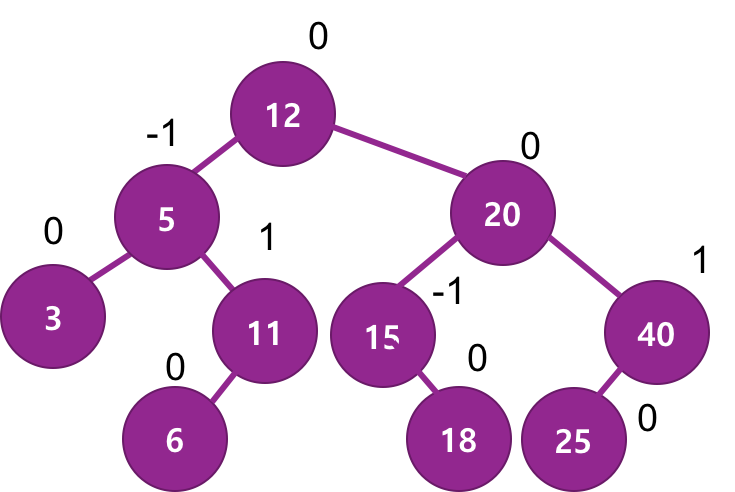
회전(rotation)
삽입 삭제시 노드들의 배열에 따라 4가지(LL, RR, LR, RL) 불균형이 발생할 수 있으며 각 상황마다 rotation에 방향을 달리하여 트리의 균형을 맞춥니다.
- LL(Left Left) case
- y는 z의 왼쪽 자식 노드이고, x는 y의 왼쪽 자식 노드인 경우 right rotation
- y노드의 오른쪽 자식 노드를 z노드로 변경 - z노드 왼쪽 자식 노드를 y노드 오른쪽 서브트리(T2)로 변경

- RR(Right Right) case
- y는 z의 오른쪽 자식 노드이고, x는 y의 오른쪽 자식 노드인 경우 left rotation
- y노드의 왼쪽 자식 노드를 z노드로 변경 - z노드 오른쪽 자식 노드를 y노드 왼쪽 서브트리(T2)로 변경

- LR(Left Right) case
- y는 z의 왼쪽 자식 노드이고, x는 y의 오른쪽 자식 노드인 경우 left , right 순으로 총 두 번의 rotation을 수행

- RL(Right Left) case
- y는 z의 오른쪽 자식 노드이고, x는 y의 왼쪽 자식 노드인 경우, right, left 순으로 총 두번의 rotation을 수행

삽입/삭제 연산
AVL 트리의 삽입 연산은 기본적으로 이진탐색트리와 동일합니다.
Heap
- 데이터에서 최대값과 최소값을 빠르게 찾기 위해 고안된 완전 이진 트리(Complete Binary Tree)
- 시간복잡도: O(logn)
- 최소힙(Min Heap), 최대힙(Max Heap)
트라이(Trie, 접두사 트리 = Prefix Tree)
- 각 노드의 문자를 저장하는 자료구조
- 트리를 아래쪽으로 순회하면 단어가 나온다.
- 접두사를 빠르게 찾아보기 위한 방식, 모든 언어를 트라이에 저장해 놓는 방식
- 문자열을 빠르게 탐색할 수 있는 자료구조
- 시간복잡도: O(M)
class Trie:
head = dict()
def add(self, word):
cur = self.head
for ch in word:
if ch not in cur:
cur[ch] = {}
cur = cur[ch]
cur['*'] = True
def search(self, word):
cur = self.head
for ch in word:
if ch not in cur:
return False
cur = cur[ch]
if '*' in cur:
return True
else:
return False
dictionary = Trie()
dictionary.add('hi')
dictionary.add('hello')
print(dictionary.search('hi')) # True
print(dictionary.search('hello')) # True
print(dictionary.search('hey')) # False